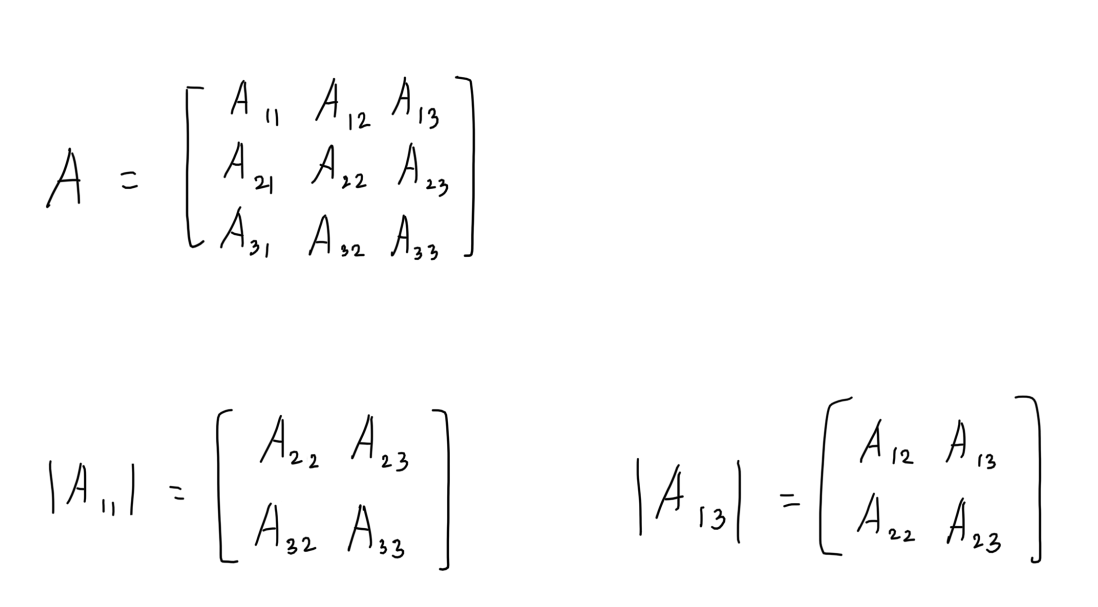게임 개발 블로그

선형변환의 정의 3차원 벡터 하나를 받아서 3차원 벡터 하나를 산출하는 함수 t(v)에서, 다음의 조건을 만족할 때, t를 가리켜 선형변환이라고 부른다. t(u+v) = t(u) + t(v) t(ku) = kt(u) 여기서 u와 v는 벡터고, k는 스칼라이다! 예를 들어서, 함수 t(x,y,z)=(x², y², z²) 일때, 스칼라 k=2와 u=(1,2,3)에 대해 선형변환이 아니다. 왜냐하면 t(2u) = t(2,4,6) = (4,16,36)이지만 2t(u) = 2(1,4,9) = (2,8,18) 이기 때문에 위에 조건에서 2번을 만족하지 않기 때문이다. 그리고 t가 선형변환이면, t(au+bv+cw) = t(au+(bv+cw)) = at(u) + t(bv+cw) = at(u) + bt(v) + ct(..

행렬 대수는 나눗셈 연산을 정의하진 않지만, 곱셈에 관한 역, 즉 역행렬에 대한 정의는 존재한다. 역행렬에 관해 중요한 정보 5가지 오직 정사각행렬만이 역행렬은 가진다. n*n행렬 M의 역은 n*n 행렬이다. 모든 정사각행렬에 역행렬이 존재하지는 않는다. 역행렬이 있는 행렬을 가리켜 가역행렬이라고 부르고, 역행렬이 없는 행렬을 특이행렬이라 부른다. 역행렬이 존재하는 경우 그 역행렬은 고유하다. 행렬에 그 역행렬을 곱하면 단위행렬이 나온다. 이때 교환법칙이 성립한다. 딸림행렬과 행렬식을 이용해서 역행렬을 구할 수 있으며, 공식은 다음과 같다. $$ A^{-1} = \frac{adj(A)}{det A} $$ 4*4 이하의 작은 행렬에서는 딸림행렬을 이용한 계산법이 효율적이고, 더 큰 행렬의 경우에는 가우스 ..

행렬식은 정사각행렬을 받아서 실수값을 산출하는 특별한 함수이다. 정사각행렬의 행렬식을 흔히 det A라고 표기한다. 실제로 행렬식은 위키피디아의 설명에 따르면 "정사각 행렬에 스칼라를 대응시키는 함수의 하나"라고 설명하며, 행렬마다 갖고있는 특정한 값을 나타낸다. 행렬식은 연립일차방정식의 해를 구하기 위해 고안되었다고 하고, 크레마의 법칙을 이용해서 연립일차방정식을 푸는데 쓰인다고 한다! 기하학적으로 행렬식은 상자의 부피와 관련이 있고.. 어쨌든 이 책에서 행렬식은 행렬의 역을 구할때 행렬식이 쓰인다고 한다. 소행렬 n*n 인 정사각행렬 A가 주어졌을 때, A의 소행렬 |Aij|는 A의 i번째 행과 j번째 열을 삭제한 결과로 생긴 (n-1) * (n-1) 행렬이다. 예를들어, 3*3 정사각행렬 A의 소행..

전치행렬 전치행렬은 주어진 행렬의 행들과 열들을 맞바꾼 것을 말한다. 따라서 m*n 행렬의 전치는 n*m 이고, 행렬 M의 전치행렬을 $$ M^{T} $$ 으로 표기한다. 예를들어, 행렬 A의 전치행렬 At는 다음과 같다. $$ A = \begin{bmatrix} 1& 3 & 8 \\ 4 & -5 & 9 \\ \end{bmatrix} $$ $$ A^{T} = \begin{bmatrix} 1&4\\ 3& -5\\ 8& 9\\ \end{bmatrix} $$ 전치행렬의 속성 전치행렬에는 다음과 같은 유용한 속성이 있다. $$ 1. (A+B)^{T} = A^{T} + B^{T} $$ $$ 2. (cA)^{T} = cA^{T} $$ $$ 3. (AB)^{T} = B^{T}A^{T} $$ $$ 4.(A^{T})^{..

컴퓨터 그래픽스에서 행렬은 비례, 회전, 이동같은 기하학적 변환을 간결하게 서술하는데 쓰이고, 점이나 벡터의 좌표를 한 기준계에서 다른 기준계로 변환하는데 쓰인다. 행렬의 정의 m * n 행렬은 m개의 행과 n개의 열로 이루어진 실수들의 정사각 배열이다. 행렬에서, 행들의 개수와 열들의 개수를 곱한 것을 행렬의 차원이라고 부른다. 그리고 행렬을 구성하는 수들을 원소 또는 성분이라고 부른다. 행벡터와 열벡터 $$ u = \begin{bmatrix} u1 & u2 & u3 &u4 \\ \end{bmatrix} $$ $$ v = \begin{bmatrix} 1\\ 2 \\ 4 \end{bmatrix} $$ 위의 행렬 u와 v는 각각 행과 열이 하나인데, 이런 종류의 행렬을 행벡터나 열벡터 라고 부른다. 얘네들..

위치벡터 3차원 그래픽 프로그램에서 공간안에 어떤 위치를 지정할 수 있어야 한다. 그렇기에 한 벡터를 위치를 지정하는데 사용할 수 있는데, 이러한 용도로 쓰이는 벡터를 위치벡터라고 한다. 따라서 위치벡터에서 중요한 것은 방향이나 크기가 아니라 벡터의 머리끝 좌표이다. 점을 벡터로 표현하는 방식을 쓰면, 벡터 연산들을 활용할 수 있다. 또한 벡터처럼 점의 위치도 어떤 특정한 좌표계에 상대적이며, 벡터 대수 자체에 이러한 개념이 딸려있기에 추가적인 작업을 해 줄 필요는 없다.

외적 내적과 다른 벡터 곱셈으로 외적이 있다. 결과가 스칼라인 내적과는 다르게 외적의 결과는 벡터이다. 또한 외적은 오직 3차원 벡터에 대해서만 정의된다. 두 3차원 벡터 u와 v에 외적을 취하면 u와v 모두에게 직교인 벡터 w가 나온다. u=(ux,uy,uz), v=(vx,vy,vz) 라고 할때, u⊗v = (uy·vz - uz·vy, uz·vx - ux·vz, ux·vy-uy·vx) 로 나타낼 수 있다! 외적에서는 교환법칙이 적용되지 않는다. 즉 u⊗v != v⊗u 이다. 또한 u⊗v = -v⊗u이다. 2차원 유사 외적 외적을 이용하면, 2개의 3차원 벡터에 직교인 벡터를 구할 수 있다. 2차원에서는 2차원 유사외적을 통해, 하나의 2차원 벡터 u=(ux,uy)에 수직인 벡터 v=(-uy,ux)를 구..

벡터의 내적 내적은 스칼라 값을 내는 벡터 곱셈의 일종이다. u = (ux,uy,uz), v = (vx,vy,vz) 라고 할때, 내적은 다음과 같다. u·v = ux·vx + uy·vy + uz·vz 이런 정의만 봐서는 내적의 기하학적 의미가 분명하지 않지만, u·v = ||u|| ||v|| cosθ 로 보면 내적이 두 벡터 사이각의 코사인을 벡터 크기들로 비례시키 것임을 알 수 있다. 특히 벡터 u와 v가 단위벡터일 때, u와 v의 내적은 두 벡터 사이각도의 코사인이다. (즉 u·v=cosθ) 따라서 다음과 같은 유용한 기하학적 속성들을 이끌어 낼 수 있다. u·v = 0 이라면, 두 벡터는 직교한다. (cosθ =0이라면 θ= 90도이니깐) u·v > 0 이라면, θ는 90도보다 작다. u·v < 0..

벡터의 크기 벡터의 크기는 해당 선분의 길이이고, 백터의 크기는 이중 수직선으로 표기한다. (u의 크기는 ||u||로 표기) 2차원 벡터에서, 피타고라스의 정리를 통해 벡터의 크기를 구할 수 있고, 3차원 벡터에서도 피타고라스의 정리를 두번 적용하면 3차원 벡터의 길이를 구할 수 있다. $$||u|| = \sqrt{x^{2}+y^{2}+z^{2}}$$ 벡터의 정규화 벡터는 크기와 방향을 가지는 값이지만, 순수하게 방향을 나타내는 용도로 사용할때, 벡터의 길이가 중요하지 않을 수 있다. 그럴때 벡터의 길이를 단위 길이가 되게해서 단위벡터로 만드는 것을 벡터의 정규화라고 한다. 벡터의 각 성분을 벡터의 크기로 나누면 벡터를 정규화 할 수 있다. $$\frac{u}{||u||}=(\frac{x}{||u||},..

벡터 벡터란 크기랑 방향을 모두 가진 수량을 가리키는 말이다. 대표적인 예시로 힘, 속도등이 있고, 3차원 게임에서는 플레이어가 보는 방향이나 광선이 이동하는 방향 등 순수하게 방향만 사용해는 경우에도 벡터를 사용한다. 벡터는 그려진 위치는 중요하지 않고, 두 벡터가 오직 길이가 같고 같은 방향을 가리킬 때에만 상등이다. 벡터와 좌표계 컴퓨터는 벡터를 기하학적으로 다루지 못하기 때문에, 벡터를 수치적으로 지정하는 방법이 필요하다. 그렇기에, 3차원 좌표계에 벡터의 꼬리를 원점으로 이동시키면 벡터를 v=(x,y,z)와 같은 좌표로 표기할 수 있다. 이때 같은 벡터라도 기준계가 다르면 좌표 표현이 달라질 수도 있다. 하지만 벡터의 방향과 크기는 변하지 않고, 좌표계에 따라 바뀌는건 벡터를 표현하는 좌표뿐이다..