외적
내적과 다른 벡터 곱셈으로 외적이 있다.
결과가 스칼라인 내적과는 다르게 외적의 결과는 벡터이다.
또한 외적은 오직 3차원 벡터에 대해서만 정의된다.
두 3차원 벡터 u와 v에 외적을 취하면 u와v 모두에게 직교인 벡터 w가 나온다.
u=(ux,uy,uz), v=(vx,vy,vz) 라고 할때,
u⊗v = (uy·vz - uz·vy, uz·vx - ux·vz, ux·vy-uy·vx)
로 나타낼 수 있다!
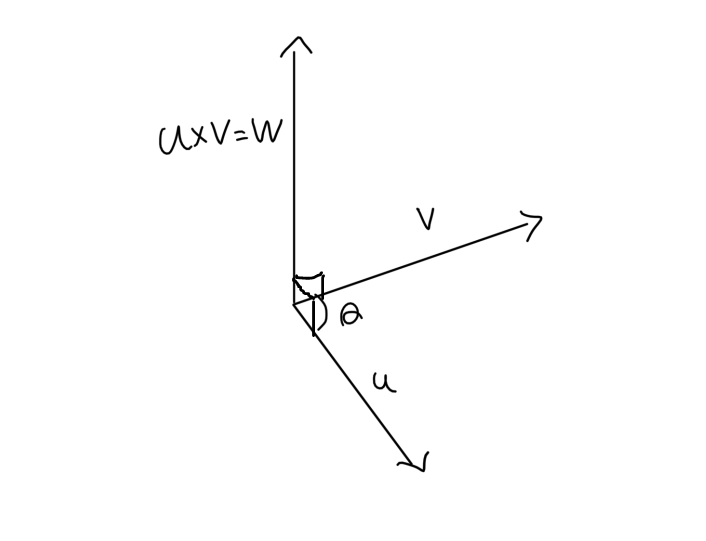
외적에서는 교환법칙이 적용되지 않는다.
즉 u⊗v != v⊗u 이다.
또한 u⊗v = -v⊗u이다.
2차원 유사 외적
외적을 이용하면, 2개의 3차원 벡터에 직교인 벡터를 구할 수 있다.
2차원에서는 2차원 유사외적을 통해,
하나의 2차원 벡터 u=(ux,uy)에 수직인 벡터 v=(-uy,ux)를 구하는 것은 가능하다.
'컴퓨터 그래픽스' 카테고리의 다른 글
| 2. 행렬 대수 : 정의 (0) | 2023.03.28 |
|---|---|
| 1. 벡터 대수 : 점 (0) | 2023.03.23 |
| 1. 벡터 대수 : 내적 (0) | 2023.03.23 |
| 1. 벡터 대수 : 길이와 단위벡터 (0) | 2023.03.23 |
| 1. 벡터 대수 : 벡터 (0) | 2023.03.23 |