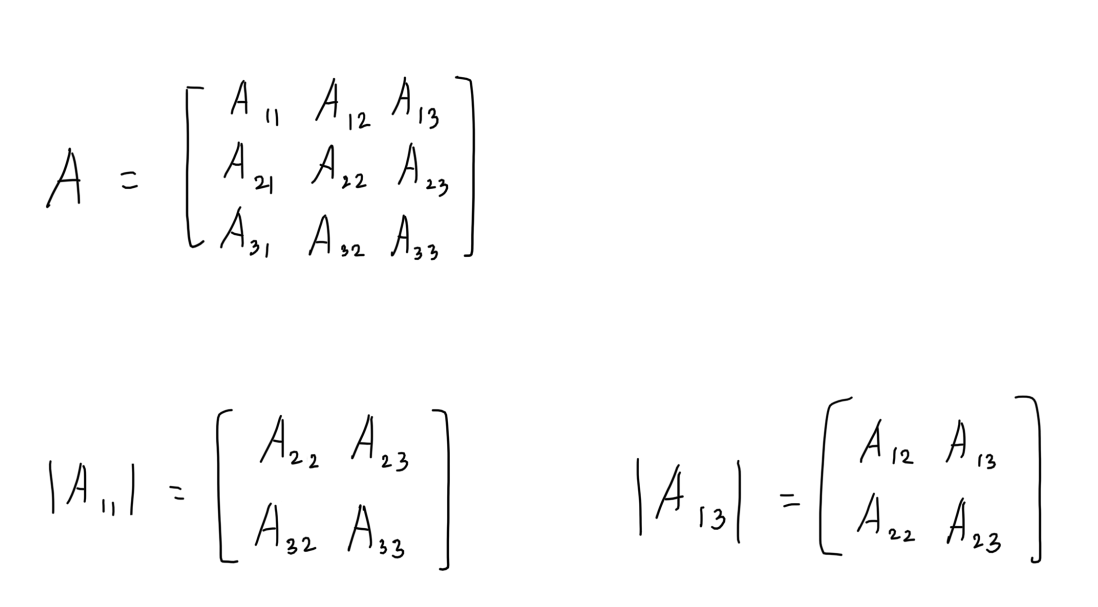게임 개발 블로그

S가 비례행렬, R이 회전행렬, T가 이동행렬이라고 할 때, 여덟개의 정점 vi로 이루어진 직육면체의 각 정점에 이 세 변환을 연달아 적용한다고 가정한다. ((viS)R)T = (vi'R)T = vi''T = vi''' 그런데 행렬 곱셈은 결합법칙을 만족하기에, 다음과 같이 표기할 수 있다. vi(SRT) = vi''' 즉 행렬 C= SRT, 세개의 변환을 행렬 곱셈을 이용해서 하나의 변환으로 결합할 수 있다. 이렇게 결합하면 더 좋은 성능을 낼 수 있다! 위의 경우처럼 8개의 정점을 가진 직육면체에 처음처럼 3가지 변환을 연달아 적용한다면, 벡터행렬 곱셈이 3*8번 필요하다. 그러나 결합된 행렬방식으로 계산하면, 행렬행렬 곱셈 두번과 벡터행렬 곱셈 8번이면 된다.

동차좌표 아핀변환이란 선형변환에 이동이 결합된 것이다. 그런데 선형변환은 벡터로 이루어져 있다. 벡터는 오직 방향과 크기만 서술하기에, 벡터는 이동에 대해 불변이여야 한다. 즉, 이동(위치벡터)는 오직 점에만 적용되어야 한다.. 이때, 동차좌표를 사용해서 점과 벡터를 동일한 방식으로 다룰 수 있다. 동차 좌표란 어떤 목적을 가지고 한 차원을 추가해 표현하는 것을 말한다. 한마디로 3차원 벡터에 w 성분을 추가한 것이다! 동차좌표의 형태는 1. 벡터의 경우 : (x,y,z,0) 2. 점의 경우 : (x,y,z,1) 아핀변환의 정의 및 행렬 표현 위에서도 말했지만, 아핀변환은 선형변환에 이동 벡터 b를 더한것이다. a(u) = t(u) +b 로 나타낼 수 있다! 이를 행렬로 표현하면.. 이때 w=1인 동차좌..

선형변환의 정의 3차원 벡터 하나를 받아서 3차원 벡터 하나를 산출하는 함수 t(v)에서, 다음의 조건을 만족할 때, t를 가리켜 선형변환이라고 부른다. t(u+v) = t(u) + t(v) t(ku) = kt(u) 여기서 u와 v는 벡터고, k는 스칼라이다! 예를 들어서, 함수 t(x,y,z)=(x², y², z²) 일때, 스칼라 k=2와 u=(1,2,3)에 대해 선형변환이 아니다. 왜냐하면 t(2u) = t(2,4,6) = (4,16,36)이지만 2t(u) = 2(1,4,9) = (2,8,18) 이기 때문에 위에 조건에서 2번을 만족하지 않기 때문이다. 그리고 t가 선형변환이면, t(au+bv+cw) = t(au+(bv+cw)) = at(u) + t(bv+cw) = at(u) + bt(v) + ct(..

장애물 생성 장애물을 만들기 위해, 우선 장애물 역할을 할 바위를 그렸다.. using System.Collections; using System.Collections.Generic; using UnityEngine; public class ObstacleGenerator : MonoBehaviour { public GameObject obstacle; public GameObject testTerrain; public void CreateObstacle(GameObject terrain) { Vector2[] points = terrain.GetComponent().points; int randomPoint = Random.Range(2, points.Length - 2); Vector3 obstacl..

행렬 대수는 나눗셈 연산을 정의하진 않지만, 곱셈에 관한 역, 즉 역행렬에 대한 정의는 존재한다. 역행렬에 관해 중요한 정보 5가지 오직 정사각행렬만이 역행렬은 가진다. n*n행렬 M의 역은 n*n 행렬이다. 모든 정사각행렬에 역행렬이 존재하지는 않는다. 역행렬이 있는 행렬을 가리켜 가역행렬이라고 부르고, 역행렬이 없는 행렬을 특이행렬이라 부른다. 역행렬이 존재하는 경우 그 역행렬은 고유하다. 행렬에 그 역행렬을 곱하면 단위행렬이 나온다. 이때 교환법칙이 성립한다. 딸림행렬과 행렬식을 이용해서 역행렬을 구할 수 있으며, 공식은 다음과 같다. $$ A^{-1} = \frac{adj(A)}{det A} $$ 4*4 이하의 작은 행렬에서는 딸림행렬을 이용한 계산법이 효율적이고, 더 큰 행렬의 경우에는 가우스 ..

행렬식은 정사각행렬을 받아서 실수값을 산출하는 특별한 함수이다. 정사각행렬의 행렬식을 흔히 det A라고 표기한다. 실제로 행렬식은 위키피디아의 설명에 따르면 "정사각 행렬에 스칼라를 대응시키는 함수의 하나"라고 설명하며, 행렬마다 갖고있는 특정한 값을 나타낸다. 행렬식은 연립일차방정식의 해를 구하기 위해 고안되었다고 하고, 크레마의 법칙을 이용해서 연립일차방정식을 푸는데 쓰인다고 한다! 기하학적으로 행렬식은 상자의 부피와 관련이 있고.. 어쨌든 이 책에서 행렬식은 행렬의 역을 구할때 행렬식이 쓰인다고 한다. 소행렬 n*n 인 정사각행렬 A가 주어졌을 때, A의 소행렬 |Aij|는 A의 i번째 행과 j번째 열을 삭제한 결과로 생긴 (n-1) * (n-1) 행렬이다. 예를들어, 3*3 정사각행렬 A의 소행..

odyssey의 지형생성 방식에 대해 생각해봤는데.. 미리 여러 타입의 지형을 생성해놓고, (일단은) 런타임 중에 적당히 랜덤하게 붙이기로 했다. https://san10.tistory.com/10 #5 odyssey 개발일지 : 베지어 곡선으로 곡선 지형 생성 지금까지는 임시로 곡선 지형을 만들었는데 이제는 베지어 곡선으로 지형을 만들려고 한다. 베지어 곡선이란? n개의 조절점과 선형 보간을 통해 얻을 수 있는 곡선으로, n-1차 베지어 곡선이라고 san10.tistory.com 지난번에 지형을 생성하는 기능을 만들었기는 한데.. 그런데 문제는 스크립트로 지형을 생성하기 때문에 런타임 중에만 생성이 되고 에디터로 돌아오면 파괴되서 볼 수가 없다... 그래서 방법을 좀 찾아봤는데 에디터를 커스텀해서 에디..

전치행렬 전치행렬은 주어진 행렬의 행들과 열들을 맞바꾼 것을 말한다. 따라서 m*n 행렬의 전치는 n*m 이고, 행렬 M의 전치행렬을 $$ M^{T} $$ 으로 표기한다. 예를들어, 행렬 A의 전치행렬 At는 다음과 같다. $$ A = \begin{bmatrix} 1& 3 & 8 \\ 4 & -5 & 9 \\ \end{bmatrix} $$ $$ A^{T} = \begin{bmatrix} 1&4\\ 3& -5\\ 8& 9\\ \end{bmatrix} $$ 전치행렬의 속성 전치행렬에는 다음과 같은 유용한 속성이 있다. $$ 1. (A+B)^{T} = A^{T} + B^{T} $$ $$ 2. (cA)^{T} = cA^{T} $$ $$ 3. (AB)^{T} = B^{T}A^{T} $$ $$ 4.(A^{T})^{..

컴퓨터 그래픽스에서 행렬은 비례, 회전, 이동같은 기하학적 변환을 간결하게 서술하는데 쓰이고, 점이나 벡터의 좌표를 한 기준계에서 다른 기준계로 변환하는데 쓰인다. 행렬의 정의 m * n 행렬은 m개의 행과 n개의 열로 이루어진 실수들의 정사각 배열이다. 행렬에서, 행들의 개수와 열들의 개수를 곱한 것을 행렬의 차원이라고 부른다. 그리고 행렬을 구성하는 수들을 원소 또는 성분이라고 부른다. 행벡터와 열벡터 $$ u = \begin{bmatrix} u1 & u2 & u3 &u4 \\ \end{bmatrix} $$ $$ v = \begin{bmatrix} 1\\ 2 \\ 4 \end{bmatrix} $$ 위의 행렬 u와 v는 각각 행과 열이 하나인데, 이런 종류의 행렬을 행벡터나 열벡터 라고 부른다. 얘네들..

저번에 베지어곡선으로 지형을 생성했다. 원래 생각대로라면 런타임중에 베지어곡선으로 지형을 생성하려 했는데... 맵 생성 알고리즘을 찾아보다가 noise로 지형을 생성할 수 있다는 걸 알게되었다! perline noise 펄린 노이즈는 Ken Perline이 영화 '트론'을 제작중에 개발한 노이즈 함수이다. 유기적인 모양의 노이즈를 생성한다. 생성원리 임의의 점 x,y은 항상 그리드 안에 위치한다. 점 (x,y)을 둘러싼 그리드의 꼭지점부터 gradient 벡터를 생성한다. 이때 gradient 는 크기가 1인 벡터이고, 이는 유사 난수라고 하는데 왜냐하면 그리드당 랜덤한 벡터값을 부여하기 때문이다. 다음으로 그리드의 꼭짓점부터 점 (x,y)로 향하는 거리벡터를 계산한다. 위에서 구한 gradient 벡터..